Como encontrar o raio de um círculo: para ajudar escolares

Como encontrar o raio de um círculo? Esta questão é sempre relevante para alunos que estudam planimetria. Abaixo, vamos considerar vários exemplos de como lidar com a tarefa.

Dependendo da condição do problema, você pode encontrar o raio do círculo como este.

Fórmula 1: R = A / 2π, onde A é o comprimento do círculo, e π é uma constante igual a 3.141 ...

Fórmula 2: R = √ (S / π), onde S é a área do círculo.

Fórmula 3: R = D / 2, onde D é o diâmetro do círculo, ou seja, o comprimento do segmento que, passando pelo centro da figura, conecta dois pontos que estão tão distantes quanto possível um do outro.

Como encontrar o raio do círculo circunscrito

Primeiro, vamos definir o próprio termo. Um círculo é chamado descrito quando toca todos os vértices de um determinado polígono. Deve-se notar que é possível descrever um círculo apenas em torno de um polígono, cujos lados e ângulos são iguais uns aos outros, isto é, em torno de um triângulo equilátero, um quadrado, um rombo regular, e assim por diante. Para resolver o problema, é necessário encontrar o perímetro do polígono e também medir os lados e a área. Portanto, arme-se com uma régua, uma bússola, uma calculadora e um caderno com uma caneta.

Como encontrar o raio de um círculo, se for descrito em torno de um triângulo

Fórmula 1: R = (A * B * B) / 4S, onde A, B, B - o comprimento dos lados do triângulo e S - sua área.

Fórmula 2: R = A / sin a, onde A é o comprimento de um lado da figura, e sin a é o valor calculado do seno do ângulo oposto a este lado.

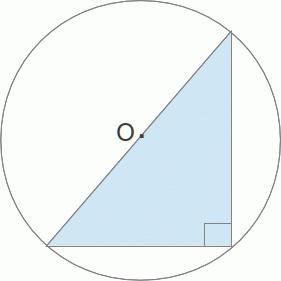
O raio do círculo, que é descrito em torno de um triângulo direito.

Fórmula 1: R = B / 2, onde B é a hipotenusa.

Fórmula 2: R = M * B, onde B é a hipotenusa, e M é a mediana desenhada para isso.

Como encontrar o raio de um círculo, se for descrito em torno de um polígono regular

Fórmula: R = A / (2 * sin (360 / (2 * n))), onde A é o comprimento de um lado da figura, e n é o número de lados em uma dada figura geométrica.

Como encontrar o raio de um círculo inscrito

Um círculo inscrito é chamado quando toca em todos os lados de um polígono. Vamos considerar alguns exemplos.

Fórmula 1: R = S / (P / 2), onde - S e P - a área e o perímetro da figura, respectivamente.

Fórmula 2: R = (P / 2 - A) * tg (a / 2), onde P - perímetro, A - o comprimento de um lado e - o ângulo oposto a este lado.

Como encontrar o raio de um círculo se ele estiver inscrito num triângulo direito

Fórmula 1:

O raio do círculo, que está inscrito no rombo

O círculo pode ser inscrito em qualquer rombo, tanto equilátero quanto não equilátero.

Fórmula 1: R = 2 * H, onde H é a altura da figura geométrica.

Fórmula 2: R = S / (A * 2), onde S é a área do diamante e A é o comprimento do seu lado.

Fórmula 3: R = √ ((S * sin A) / 4), onde S é a área do diamante, e o pecado A é o seno do ângulo agudo da figura geométrica dada.

Fórmula 4: R = B * à / (√ (² + ²), onde  e à são os comprimentos das diagonais da figura geométrica.

Fórmula 5: R = B * sin (A / 2), onde B é a diagonal do losango, e A é o ângulo nos vértices que ligam a diagonal.

O raio do círculo inscrito no triângulo

Se, na condição do problema, você receber os comprimentos de todos os lados da figura, calcule primeiro o perímetro do triângulo (P) e, em seguida, o semiperímetro (n):

P = A + B + B, onde A, B, B são os comprimentos dos lados da figura geométrica.

n = n / 2.

Fórmula 1: R = √ ((n-A) * (n-B) * (n-B) / n).

E se, conhecendo os mesmos três lados, você recebe a área da figura, então você pode calcular o raio desejado da seguinte maneira.

Fórmula 2: R = S * 2 (A + B + B)

Fórmula 3: R = S / n = S / (A + B + B) / 2), onde - n é o semiperímetro da figura geométrica.

Fórmula 4: R = (n - A) * tg (A / 2), onde n é a metade do perímetro do triângulo, A é um dos seus lados e tg (A / 2) é a tangente da metade do ângulo oposto a este lado.

E a fórmula abaixo irá ajudá-lo a encontrar o raio do círculo inscrito em um triângulo equilátero.

Fórmula 5: R = A * √3 / 6.

O raio do círculo, inscrito em um triângulo retângulo

Se no problema os comprimentos das pernas são dados, bem como a hipotenusa, então o raio do círculo inscrito é reconhecido como segue.

Fórmula 1: R = (A + B-C) ​​/ 2, onde A, B - as pernas, C - a hipotenusa.

Nesse caso, se você está apenas duas pernas, é hora de lembrar o teorema de Pitágoras para encontrar a hipotenusa e usar a fórmula acima.

C = √ (A² + B²).

O raio do círculo, inscrito na praça

O círculo, que é inscrito em um quadrado, divide todos os seus 4 lados exatamente na metade nos pontos de tangência.

Fórmula 1: R = A / 2, onde A - o comprimento do lado do quadrado.

Fórmula 2: R = S / (P / 2), onde S e P são a área e o perímetro do quadrado, respectivamente.