Polígonos convexos. Definição de um polígono convexo. Diagonais de um polígono convexo

Essas figuras geométricas nos cercam em todos os lugares. Polígonos convexos são naturais, por exemplo, favos de abelhas ou artificiais (criados por humanos). Estas figuras são usadas na produção de vários tipos de revestimentos, em pintura, arquitetura, decorações, etc. Os polígonos convexos têm a propriedade de que todos os seus pontos estão localizados em um lado da linha que passa por um par de vértices adjacentes dessa figura geométrica. Existem outras definições. Convexo é aquele polígono que está localizado em um único meio plano em relação a qualquer linha contendo um de seus lados.

Polígonos convexos

No curso da geometria elementar, sempreConsideramos apenas polígonos simples. Para entender todas as propriedades de tais figuras geométricas é necessário entender sua natureza. Para começar, deve ser entendido que qualquer linha cujas extremidades coincidem são chamadas fechadas. E a figura formada por ele pode ter uma variedade de configurações. Um polígono é uma linha poligonal fechada simples cujos links adjacentes não estão na mesma linha. Suas ligações e picos são, respectivamente, os lados e vértices dessa figura geométrica. Uma polilinha simples não deve ter auto-interseções.

Os vértices de um polígono são chamados adjacentes, em quese eles representam as extremidades de um dos seus lados. Uma figura geométrica que tenha o n-ésimo número de vértices e, portanto, o n-ésimo número de lados, é chamada de n-gon. A linha quebrada em si é chamada de limite ou contorno dessa figura geométrica. Um polígono plano ou plano poligonal é chamado de parte finita de qualquer plano delimitado por ele. Os lados vizinhos desta figura geométrica são os segmentos de uma linha quebrada a partir de um vértice. Eles não serão vizinhos se vierem de diferentes vértices do polígono.

Outras definições de polígonos convexos

Na geometria elementar, existem vários outrosequivalente em seu significado de definições, indicando qual polígono é chamado de convexo. E todas essas formulações são igualmente verdadeiras. Um polígono convexo é considerado:

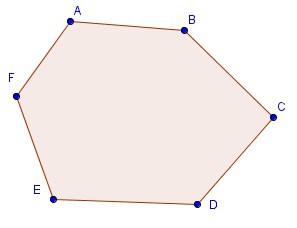
• cada segmento que conecta quaisquer dois pontos dentro dele está completamente nele;

• dentro dela estão todas as suas diagonais;

• qualquer ângulo interno não exceda 180 °.

O polígono divide sempre o plano por 2partes. Um deles é limitado (pode ser colocado em um círculo) e o outro é ilimitado. O primeiro é chamado de região interna, e o segundo é chamado de região externa dessa figura geométrica. Este polígono é a interseção (em outras palavras - o componente comum) de vários meios-planos. Nesse caso, cada segmento que termina nos pontos que pertencem ao polígono pertence completamente a ele.

Variedades de polígonos convexos

A definição de um polígono convexo não indicapara o fato de que existem muitos tipos. E cada um deles tem certos critérios. Assim, os poligonos convexos, que têm um ângulo interno de 180 °, que se refere a ligeiramente convexa. A figura geométrica convexa que tem três picos, é chamado um triângulo, quatro - quadrilátero, cinco - pentágono, etc. Cada um dos convexa n-gons satisfaz os seguintes requisitos importantes: .. n tem de ser igual ou superior a 3. Cada um dos triângulos é convexa. A figura geométrica deste tipo em que todos os vértices estão localizados em um círculo, o chamado círculo inscrito. Um polígono convexo é chamado descrito se todos os seus lados próximos ao círculo o tocarem. Dois polígonos são chamados de igual apenas no caso quando se utiliza a sobreposição podem ser combinados. polígono plano chamado plano poligonal (um troço plano) que esta figura geométrica limitada.

Polígonos convexos regulares

Polígonos corretos são chamadosfiguras geométricas com ângulos e lados iguais. Dentro deles há um ponto 0, que está na mesma distância de cada um dos seus vértices. É chamado o centro desta figura geométrica. Os segmentos que conectam o centro com os vértices dessa figura geométrica são chamados de apophemes, e aqueles que conectam o ponto 0 aos lados são raios.

O quadrilátero direito é um quadrado. O triângulo retângulo é chamado equilateral. Para essas figuras, a seguinte regra existe: cada ângulo de um polígono convexo é de 180 ° * (n-2) / n,

onde n é o número de vértices dessa figura geométrica convexa.

A área de qualquer polígono regular é definida pela fórmula:

S = p * h

onde p é igual a metade da soma de todos os lados de um determinado polígono eh é igual ao comprimento do apophema.

Propriedades de polígonos convexos

Polígonos convexos possuem certas propriedades. Assim, o segmento que conecta quaisquer dois pontos de uma figura geométrica está necessariamente localizado nela. Prova:

Suponha que P seja um dado convexopolígono. Tome dois pontos arbitrários, por exemplo, A e B, que pertencem ao P. Pela definição atual de um polígono convexo, esses pontos estão localizados em um lado da linha reta que contém qualquer direção R. Consequentemente, AB também tem essa propriedade e está contido em R. Um polígono convexo sempre pode ser dividido em vários triângulos absolutamente todas as diagonais, que realizou um de seus vértices.

Os ângulos de figuras geométricas convexas

Os ângulos de um polígono convexo são ângulos quesão formados por suas partes. Cantos internos estão na área interna dessa figura geométrica. O ângulo que é formado por seus lados, que convergem em um vértice, é chamado de ângulo do polígono convexo. Ângulos adjacentes aos ângulos internos de uma determinada figura geométrica são chamados externos. Cada ângulo de um polígono convexo localizado dentro dele é igual a:

180 ° - x,

onde x é o valor do ângulo externo. Essa fórmula simples se aplica a qualquer figura geométrica desse tipo.

No caso geral, existe para ângulos externosa seguinte regra: cada ângulo de um polígono convexo é igual à diferença entre 180 ° e o valor do ângulo interno. Pode ter valores no intervalo de -180 ° a 180 °. Portanto, quando o ângulo interno é de 120 °, o ângulo externo será de 60 °.

A soma dos ângulos de polígonos convexos

A soma dos ângulos internos de um polígono convexo é estabelecida pela fórmula:

180 ° * (n-2),

onde n é o número de vértices do n-gon.

A soma dos ângulos de um polígono convexo é computadasimplesmente. Considere qualquer figura geométrica desse tipo. Para determinar a soma dos ângulos dentro de um polígono convexo, um de seus vértices deve estar conectado a outros vértices. Como resultado dessa ação, obtemos triângulos (n-2). Sabe-se que a soma dos ângulos de qualquer triângulo é sempre de 180 °. Como seu número em qualquer polígono é igual a (n-2), a soma dos ângulos internos de tal figura é de 180 x (n-2).

A soma dos ângulos de um polígono convexo, viz.quaisquer dois ângulos externos internos e adjacentes, essa figura geométrica convexa será sempre de 180 °. A partir disso, é possível determinar a soma de todos os seus ângulos:

180 х n.

A soma dos ângulos internos é de 180 ° * (n-2). A partir daí, a soma de todos os ângulos externos da figura dada é estabelecida pela fórmula:

180 ° * n-180 ° - (n-2) = 360 °.

A soma dos ângulos externos de qualquer polígono convexo será sempre 360 ​​° (independentemente do número de seus lados).

O ângulo externo do polígono convexo é geralmente representado por uma diferença entre 180 ° e o valor do ângulo interno.

Outras propriedades de um polígono convexo

Além das propriedades básicas destas geométricasfiguras, eles têm outros que surgem quando manipulá-los. Assim, qualquer um dos polígonos pode ser dividido em vários n-gons convexos. Para isso, é necessário continuar cada um dos seus lados e cortar essa figura geométrica ao longo dessas linhas retas. Dividir qualquer polígono em várias partes convexas e de tal forma que os vértices de cada uma das peças coincidam com todos os seus vértices. A partir desta figura geométrica é muito simples fazer triângulos segurando todas as diagonais de um vértice. Assim, qualquer polígono, em última análise, pode ser dividido em um certo número de triângulos, o que é muito útil na solução de vários problemas associados a tais figuras geométricas.

Perímetro de um polígono convexo

As peças da polilinha, chamadas de ladospolígono, mais frequentemente denotado pelas seguintes letras: ab, bc, cd, de, ea. Estes são os lados da figura geométrica com os vértices a, b, c, d, e. A soma dos comprimentos de todos os lados desse polígono convexo é chamada de perímetro.

Círculo de um polígono

Polígonos convexos podem ser inscritos edescrito. Um círculo tocando todos os lados dessa figura geométrica é chamado de inscrito nela. Tal polígono é chamado descrito. O centro do círculo que está inscrito no polígono é o ponto de interseção das bissetrizes de todos os ângulos dentro de uma dada figura geométrica. A área de tal polígono é igual a:

S = p * r

onde r é o raio do círculo inscrito e p é o semiperímetro do polígono dado.

Um círculo contendo os vértices de um polígono,chamado descrito perto dele. Neste caso, esta figura geométrica convexa é chamada de inscrita. O centro do círculo, que é descrito perto de tal polígono, representa o ponto de intersecção das chamadas perpendiculares médias de todos os lados.

Diagonais de figuras geométricas convexas

Diagonais de um polígono convexo são segmentos,que conecta vértices não adjacentes. Cada um deles está dentro dessa figura geométrica. O número de diagonais de tal n-gon é estabelecido pela fórmula:

N = n (n-3) / 2.

O número de diagonais de um polígono convexo é reproduzidoum papel importante na geometria elementar. O número de triângulos (K), no qual cada polígono convexo pode ser dividido, é calculado pela seguinte fórmula:

K = n - 2.

O número de diagonais de um polígono convexo depende sempre do número de seus vértices.

Dividindo um polígono convexo

Em alguns casos, para resolveré necessário dividir um polígono convexo em vários triângulos com diagonais desarticuladas. Esse problema pode ser resolvido derivando uma fórmula definida.

Definição do problema: chamamos uma certa partição de um n-gon convexo em vários triângulos por diagonais que se cruzam apenas nos vértices dessa figura geométrica.

Solução: Suponha que P1, P2, P3 ..., Pn são os vértices deste n-gon. O número Xn é o número de suas partições. Consideramos cuidadosamente a diagonal resultante da figura geométrica Pi Pn. Em qualquer uma das partições regulares, P1 Pn pertence a um certo triângulo P1 Pi Pn, para o qual 1 <i <n. Partindo disto e assumindo que i = 2,3,4 ..., n-1, obtemos (n-2) grupos dessas partições, nas quais todos os possíveis casos especiais são incluídos.

Seja i = 2 um grupo de regularesque contém sempre a diagonal P2Pn. O número de partições que entram coincide com o número de partições do (n-1) -gon P2 P3 P4 ... Pn. Em outras palavras, é igual a Xn-1.

Se i = 3, então este outro grupo de partições serácontenha sempre as diagonais P3 P1 e P3 Pn. Além disso, o número de partições regulares contidas neste grupo coincidirá com o número de partições (n-2) -gon P3 P4 ... Pn. Em outras palavras, será igual a Xn-2.

Seja i = 4, então entre os triângulos, o regulara decomposição conterá necessariamente um triângulo P1 P4 Pn ao qual o quadrilátero P1 P2 P3 P4, (n-3) -gon P4 P5 ... Pn estará contíguo. O número de partições regulares de tal quadrilátero é igual a X4 e o número de partições do (n-3) -gon é igual a Xn-3. Com base em todos os itens acima, podemos dizer que o número total de partições regulares contidas neste grupo é Xn-3 X4. Outros grupos para os quais i = 4, 5, 6, 7 ... conterão Xn-4 X5, Xn-5 X6, Xn-6 X7 ... de partições regulares.

Seja i = n-2, então o número de partições regulares em um determinado grupo coincidirá com o número de partições em um grupo para o qual i = 2 (em outras palavras, é igual a Xn-1).

Como X1 = X2 = 0, X3 = 1, X4 = 2 ..., então o número de todas as partições de um polígono convexo é igual a:

Xn = Xn-1 + Xn-2 + Xn-3 X4 + Xn-4 X5 + ... + X5 Xn-4 + X4 Xn-3 + Xn-2 + Xn-1.

Exemplo:

X5 = X4 + X3 + X4 = 5

X6 = X5 + X4 + X4 + X5 = 14

X7 = X6 + X5 + X4 * X4 + X5 + X6 = 42

X8 = X7 + X6 + X5 * X4 + X4 * X5 + X6 + X7 = 132

O número de partições regulares que se cruzam em uma diagonal

Na verificação de casos particulares, pode-se supor que o número de diagonais de n-gon convexo é igual ao produto de todas as partições desta figura por (n-3).

Prova desta suposição: nós representamos que P1n = Xn * (n-3), então qualquer n-gon pode ser decomposto em (n-2) -triangles. Ao mesmo tempo, um deles pode ser combinado (n-3) - o quadrilátero. Junto com isso, cada quadrilátero terá uma diagonal. Como duas diagonais podem ser desenhadas nessa figura geométrica convexa, isso significa que é possível desenhar diagonais adicionais (n-3) em qualquer (n-3) -duas laparons. A partir disso, pode-se concluir que em qualquer partição regular é possível realizar diagonais (n-3) correspondentes às condições deste problema.

Área de polígonos convexos

Muitas vezes, ao resolver vários problemas, o elementargeometria, torna-se necessário determinar a área de um polígono convexo. Suponha que (Xi. Yi), i = 1,2,3 ... n seja uma seqüência de coordenadas de todos os vértices vizinhos de um polígono que não tenha auto-interseções. Nesse caso, sua área é calculada pela seguinte fórmula:

S = ½ (∑ (X_eu + X_{eu + 1}) (Y_eu + Y_{eu + 1}))

onde (X₁Y₁) = (X_{n +1}Y_{n + 1}).