Fundamentos da análise matemática. Como encontrar o derivado?

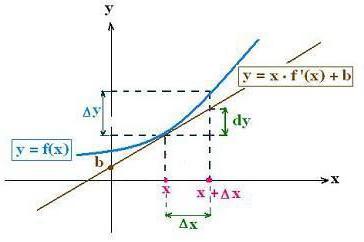
A derivada de alguma função f (x) no concretoo ponto x0 é o limite da razão entre o incremento da função e o incremento do argumento, desde que x siga para 0, e o limite exista. A derivada é geralmente denotada por um primo, às vezes por um ponto ou por um diferencial. Freqüentemente, um registro traçado através da fronteira é enganoso, uma vez que tal representação é usada extremamente raramente.

Uma função que tem um derivado em um certoponto x0, costuma-se chamá-lo diferenciável em tal ponto. Suponha que D1 seja o conjunto de pontos nos quais f é diferenciado. Atribuindo a cada número o número x pertencente a Df '(x), obtemos uma função com o domínio da notação D1. Esta função é a derivada de y = f (x). É denotado como f '(x).

Além disso, o derivado é amplamente utilizadofísica e engenharia. Vamos considerar o exemplo mais simples. O ponto do material se move ao longo do eixo de coordenadas diretamente, em que a lei do movimento é dada, isto é, a coordenada x deste ponto é a função conhecida x (t). Durante o intervalo de tempo de t0 a t0 + t, o deslocamento do ponto é x (t0 + t) -x (t0) = x, e sua velocidade média v (t) é x / t.

Às vezes o caráter do movimento é representado de tal maneira que quandoEm pequenos intervalos de tempo, a velocidade média não muda, o que significa que o movimento é considerado mais uniforme com um maior grau de precisão. Ou o valor da velocidade média, se t0 segue para algum valor absolutamente exato, que é chamado de velocidade instantânea v (t0) deste ponto em um instante específico do tempo t0. Assume-se que a velocidade instantânea v (t) é conhecida por qualquer função diferenciada x (t), com v (t) sendo igual a x '(t). Simplificando, a velocidade é a derivada da coordenada de tempo.

A velocidade instantânea tem tanto positiva quantovalores negativos, e o valor de 0. Se é em um determinado intervalo de tempo (T1, T2) é positiva, então o ponto se move na mesma direcção, isto é, x (t) coordenar aumenta com o tempo, enquanto que se v (t) for negativo, então x (t) diminui de coordenadas.

Em casos mais complexos, o ponto se move em um plano ou no espaço. Então a velocidade é uma grandeza vetorial e determina cada uma das coordenadas do vetor v (t).

Da mesma forma, você pode comparar com a aceleraçãomovimentos de ponto. A velocidade é uma função do tempo, isto é, v = v (t). E a derivada de tal função é a aceleração do movimento: a = v ’(t). Ou seja, a derivada da velocidade ao longo do tempo é uma aceleração.

Suponha que y = f (x) - qualquer diferencialfunção. Então podemos considerar o movimento de um ponto material ao longo de uma linha coordenada, que ocorre além da lei x = f (t). O conteúdo mecânico da derivada permite apresentar uma interpretação visual dos teoremas do cálculo diferencial.

Como encontrar um derivado? Encontrar a derivada de uma função é chamado de diferenciação.

Vamos dar exemplos de como encontrar a função derivada:

A derivada de uma função constante é zero; a derivada da função y = x é igual a um.

E como encontrar a derivada de uma fração? Para fazer isso, considere o seguinte material:

Para qualquer x0 <> 0, teremos

y / x = -1 / x0 * (x + x)

Existem várias regras para encontrar um derivado. A saber:

Se as funções A e B forem diferenciadas em x0,então a soma deles é diferenciada no ponto: (A + B) '= A' + B '. Simplificando, a derivada da soma é igual à soma das derivadas. Se a função é diferenciada em algum ponto, então seu incremento deve ser zero quando o incremento do argumento for para zero.

Se as funções A e B forem diferenciadas em x0,então seu produto é diferenciado no ponto: (A * B) '= A'B + AB'. (Os valores das funções e suas derivadas são calculados no ponto x0). Se a função A (x) é diferenciada em x0 e C é constante, então a função CA é diferenciada nesse ponto e (CA) ’= CA’. Ou seja, tal fator constante é retirado para o sinal da derivada.

Se as funções A e B forem diferenciadas em x0 e a função B não for igual a zero, então a proporção delas também será diferenciada no ponto: (A / B) ’= (A'B-AB’) / B * B.